Research Projects

Imporving Particle Filters using Deep Probabilistic Models
Stanford University (January 2024 - Present)
Advisor(s): Prof. Eric Darve, Prof. Daniel Tartakovsky,
The research centers on utilizing deep probabilistic models to enhance the efficiency of particle filters while addressing the well-known issue of filter divergence in high-dimensional state spaces.

System Identification under Binary Observations
Stanford University (October 2023 - Present)
Advisor(s): Prof. Wei Kang, Prof. Daniel Tartakovsky,
The research is focused on evaluating the identifiability of system states and parameters when dealing with binary observations and deriving effective strategies that maximize the utility of the limited information provided by binary observations.

Kinetic Defect for Hyperbolic Conservation Laws
Stanford University (January 2023 - August 2023)
Advisor(s): Prof. Daniel Tartakovsky,
(Under Review)
The research delves into the linear representation of conservation laws provided by kinetic formulation, specifically for problems with discontinuous solutions. It looks at a procedure to identify the kinetic defect measure, proven to exist (given the entropy solution exists) but analytically unknown. Successful identification of the kinetic defect measure provides an alternate representation of shock features, which is valuable for handling shock position-based observations in Feature-Informed Data Assimilation (FIDA).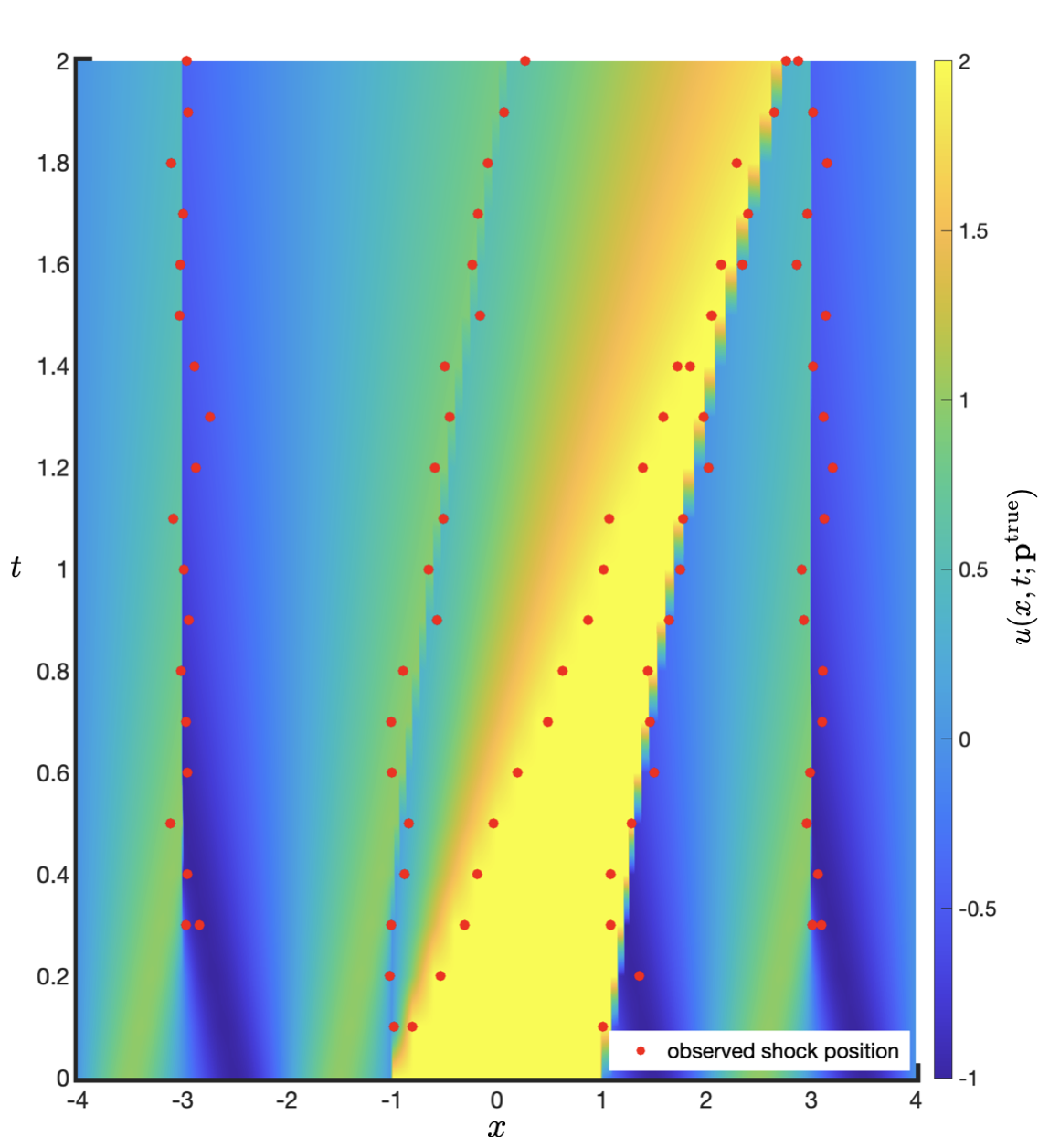

Feature-Informed Data Assimilation
Stanford University (April 2022 - January 2023)
Advisor(s): Prof. Wei Kang, Prof. Daniel Tartakovsky,
(Paper, Github)
Introduced a mathematical formulation of feature-informed data assimilation (FIDA) that leverages information from distinctive events, such as shock waves, level curves, wavefronts, and peak values in dynamical systems to estimate state variables and unknown parameters. Unlike conventional data assimilation methods, FIDA employs a set-valued functional as its observation operator, incorporating a search process over a function of state variables. The FIDA's ability to accurately estimate model parameters under noisy feature observations using Particle Filter (PF) is demonstrated through three numerical experiments.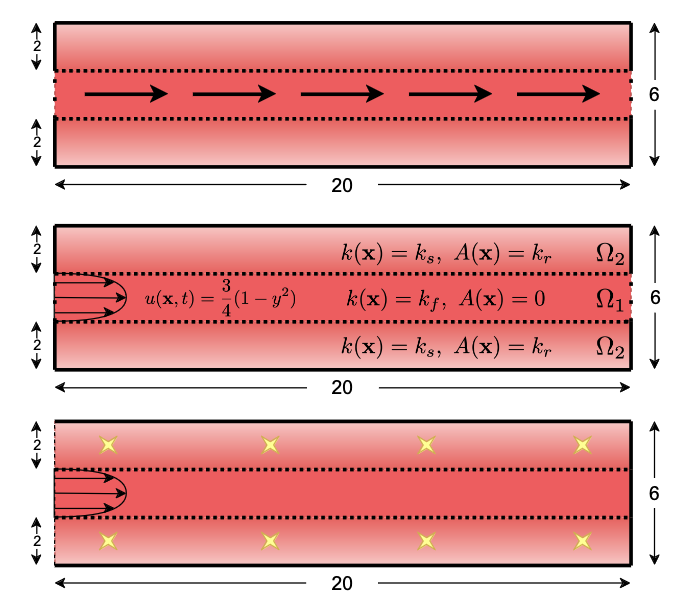

Metabolite Dynamics in the Brain
Stanford University (January 2023 - Present)
Advisor(s): Dr. Juliane Krueger, Prof. Daniel Tartakovsky,
The project presents a data assimilation strategy aimed at inferring metabolite dynamics from direct, in vivo measurements of concentration at the cellular scale. Mesoscopic model involves partial-differential equations describing convection-diffusion-consumption in the cortex and is addressed using Finite Element Method (FEM). The data assimilation effort handles uncertainties using Bayesian model averaging/selection frameworks.

Identifying reaction dynamics in the Hyporheic zone
Stanford University (July 2024 - Present)
Advisor(s): Prof. Daniele Tonina, Prof. Daniel Tartakovsky,
Developing regression models to capture the chemical dynamics within the hyporheic zone (the interface between the riverbed and groundwater) by integrating experimental data with known physical principles. These models are being used to estimate key parameters and quantify uncertainty, enhancing the understanding of complex subsurface processes. (image courtsey - Trout Unlimited Canada Facebook page)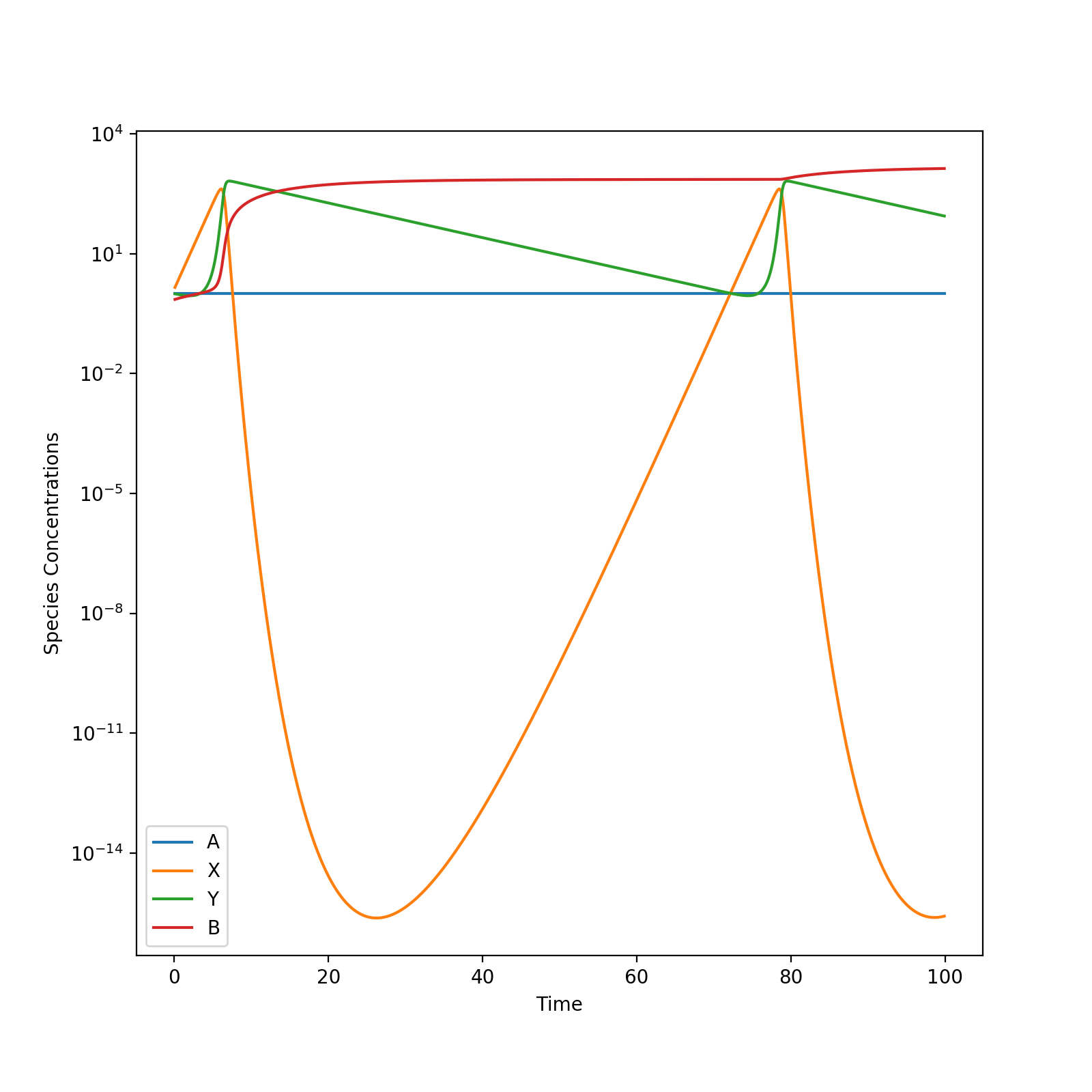

Parameter Estimation in Stiff Systems
Graduate Student Researcher
Los Alamos National Lab (July 2023 - September 2023)
Advisor(s): Dr. Balasubramanya T. Nadiga,
The study focused on exploring techniques for parameter estimation in stiff systems using temporally sparse observation data. The study used a cyclic Lotka-Volterra reaction model varying over six orders of magnitude to emulate a stiff system and identified the limitations of unscented- and ensemble-Kalman filters in addressing these estimation challenges. Following this, optimization-based (variational) data assimilation methods were used to successfully identify uncertain parameters.

Mechanical Metamaterials, Non-Affine Deformations and Deployable Structures
IIT Bombay (August 2018 - May 2020)
Advisor(s): Prof. Mandar M. Inamdar,
(Project Report)
The project started with exploring several fascinating concepts including kinetic mechanisms, origami, topological insulators, form-finding, metamaterials, and topological mechanics. The deployment of origami based models were studied using the energy profiles of the corresponding truss model. Following this, a spring ball model of plate was developed which helped in studying deformations under non-trivial strain fields.

Active Structures - Design and Control
Undergraduate Student Researcher
Applied Computing and Mechanics Laboratory, EPFL (May 2019 - July 2019)
Advisor(s): Dr. Gennaro Senatore, Prof. Ian F. C. Smith,
(Paper 1, Paper 2)
The project was directed towards developing design and control methodology for an adaptive bridge prototype. Adaptive structures are the one which undergo controlled shape changes to achieve a configuration which maximizes the efficiency of the structure in carrying the applied load. As a result of this improved efficiency, significant material and energy savings can be achieved.

Stress Ratio based Structural Optimization using Genetic Algorithm
Stanford University (July 2017 - August 2018)
Advisor(s): Prof. Venkata S. K. Delhi, Prof. Yogesh M. Desai,
This project involved using Genetic Algorithm (GA) to optimize a Fiber Reinforced Plastic based structure with more than 13,000 members. The stress-based Member Utilization Ratio served as the fitness function for population evaluation and reproduction. Various optimization algorithms, including Simplex method, Newton-Ralphson, Conjugate Gradient, Sequential Quadratic Programming, Simulated Annealing, and GA, were learned and implemented.

Academic Projects

Diffusion Model for Learned Optimizers

Stanford University (September 2023 - December 2023)

Course : Deep Generative Models

(Project Report, Github)

The project focuses on solving ill-conditioned inverse problems prevalent in engineering using Denoising Diffusion Probabilistic Models (DDPMs). Unlike deterministic optimization, our probabilistic approach captures the diverse solutions inherent in these problems. By leveraging conditional DDPMs, it offer a principled method for sampling multiple solutions, providing versatility and reliability. Our work demonstrates promising results in estimating 3D human pose from 2D keypoints, showcasing the effectiveness of our transformer-based design.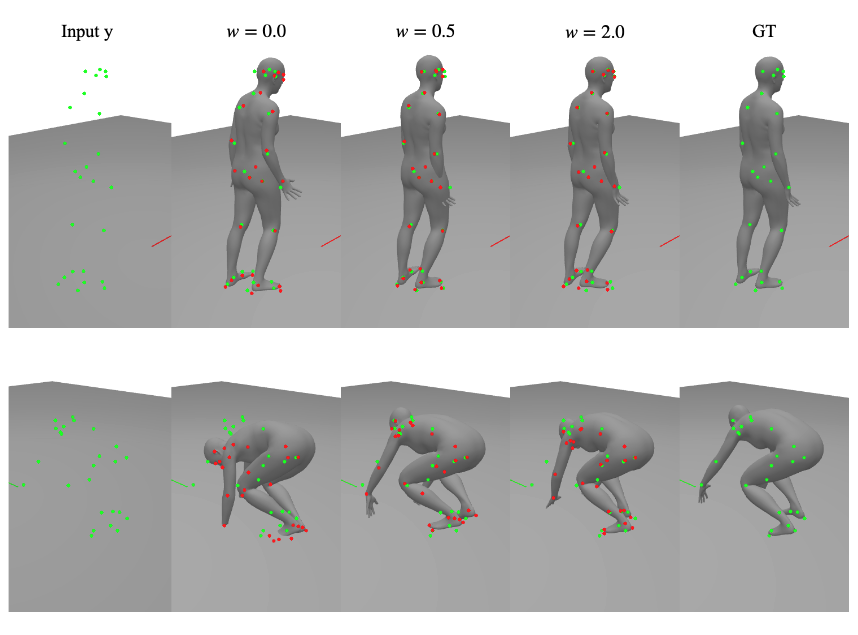

Optimal Control for Grid Balancing

Stanford University (April 2023 - June 2023)

Course : Optimal & Learning-based Control

(Project Report, Github)

This work considers an electric power grid connected to multiple houses equipped with solar electric systems and rechargeable batteries and focuses on optimizing the charge-discharge policy of rechargeable batteries under uncertainties and variability in the demand and solar power generated. The discretized problem is solved using Model Predictive Control (MPC) in conjunction with convex programming. A linear approximation of the battery dynamics is utilized to ensure feasibility and safety constraints.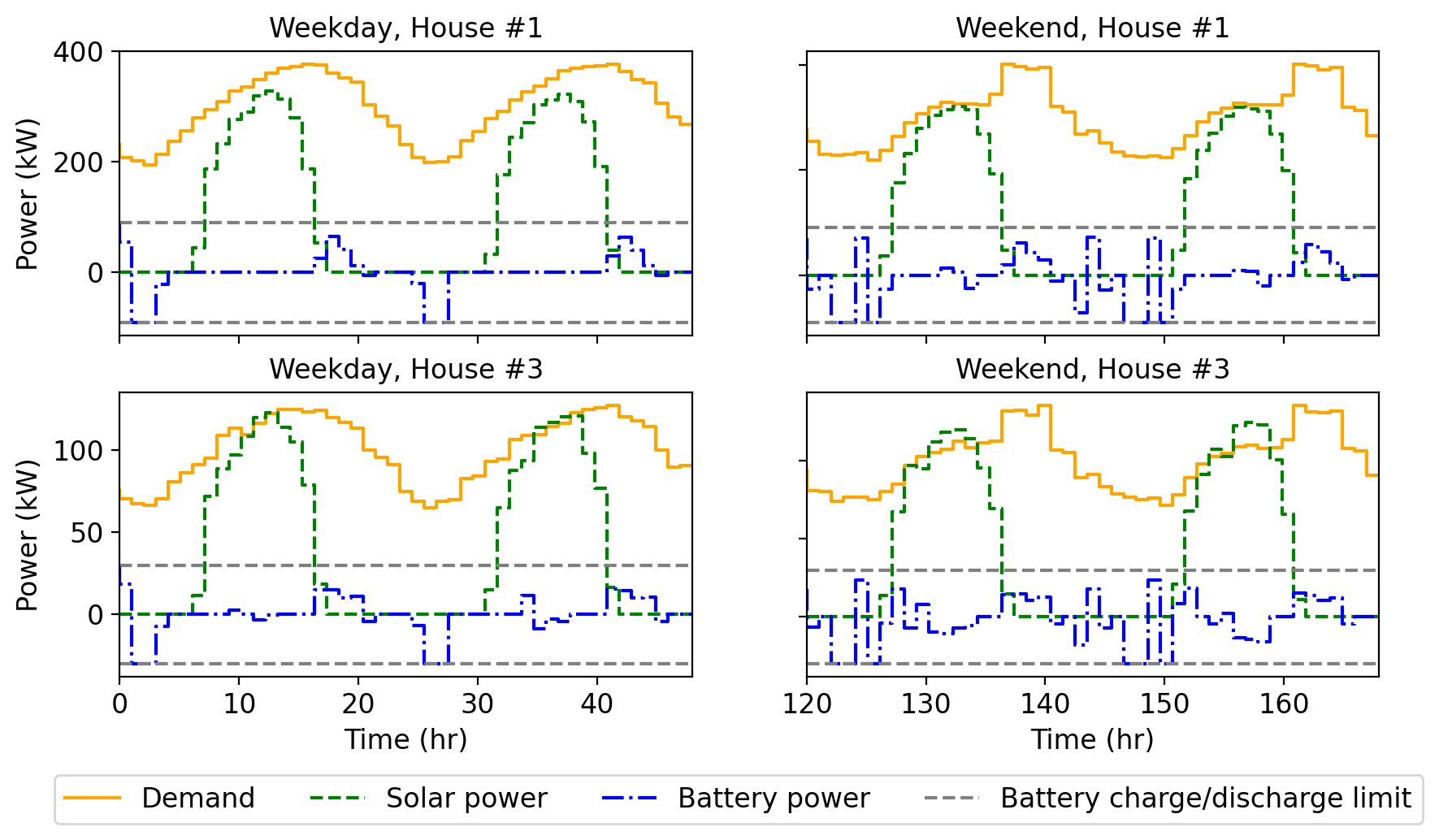

Shape of the Strongest Column

IIT Bombay (July 2018 - November 2018)

Course : Optimization, IIT Bombay

The project aimed to identify optimal column shapes of fixed volume under compressive loading with crushing and buckling constraints. The governing eigenvalue problem for identifying buckling load was developed by incorporating geometric stiffness and element stiffness matrix. The variation of the column's cross-section along its length was achieved through a Genetic Algorithm. This approach allowed for discovering optimal column shapes tailored to specific loading conditions.